I have created this example to remind myself of how to go about determining the weights and biases in an Artificial Neural Network (ANN). Calculating this is not something I regularly do. So, this is just a quick refresher in case I forget. Let’s get to it!
Imagine we are going to feed 2 inputs through an ANN with 1 hidden layer. Layer 1 has 2 neurons; with a softmax output layer with 1 neuron that provides a binary output. A visual example is shown below. How many weights and biases exist in our neural network?
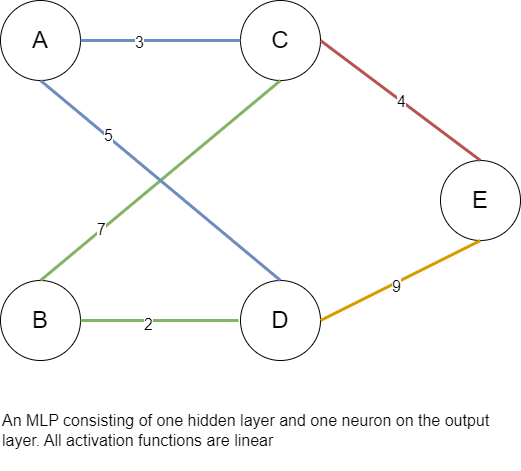
Biases
The biases are based on the number of neurons in the layers.
| Layer | Bias |
| Hidden layer (C and D) | 2 |
| Output layer (E) | 1 |
| Total | 3 |
Weights
The weights are applied to the connections between inputs and layers.
| Connections | Weights |
| Between the input layer and the first hidden layer (2 * 2) || AC+AD+BC+BD | 4 |
| Between the hidden layer and the output layer (2 * 1) || CE+DE | 2 |
| Total | 6 |
So, in the diagram above we have a total of 3 biases and 6 weights. Why is this relevant? This only becomes relevant when we consider the process of backpropagation. It is how a neural network learns, and it does this by adjusting the eights across the various neurons so that it reduces the error loss generated by the neural network.
Leave a Reply